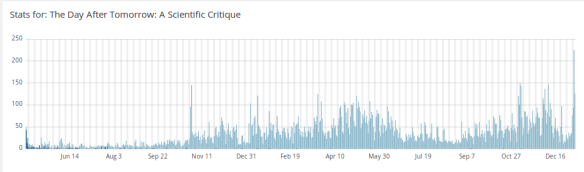
I was scanning my blog stats the other day – partly to see if people were reading my new post on the Blue Mountains bushfires, partly because I just like graphs – when I noticed that an article I wrote nearly two years ago was suddenly getting more views than ever before:
The article in question highlights the scientific inaccuracies of the 2004 film The Day After Tomorrow, in which global warming leads to a new ice age. Now that I’ve taken more courses in thermodynamics I could definitely expand on the original post if I had the time and inclination to watch the film again…
I did a bit more digging in my stats and discovered that most viewers are reaching this article through Google searches such as “is the day after tomorrow true”, “is the day after tomorrow likely to happen”, and “movie review of a day after tomorrow if it is possible or impossible.” The answers are no, no, and impossible, respectively.
But why the sudden surge in interest? I think it is probably related to the record cold temperatures across much of the United States, an event which media outlets have dubbed the “polar vortex”. I prefer “Arctic barf”.
Part of the extremely cold air mass which covers the Arctic has essentially detached and spilled southward over North America. In other words, the Arctic has barfed on the USA. Less sexy terminology than “polar vortex”, perhaps, but I would argue it is more enlightening.
Greg Laden also has a good explanation:
The Polar Vortex, a huge system of swirling air that normally contains the polar cold air has shifted so it is not sitting right on the pole as it usually does. We are not seeing an expansion of cold, an ice age, or an anti-global warming phenomenon. We are seeing the usual cold polar air taking an excursion.
Note that other regions such as Alaska and much of Europe are currently experiencing unusually warm winter weather. On balance, the planet isn’t any colder than normal. The cold patches are just moving around in an unusual way.
Having grown up in the Canadian Prairies, where we experience daily lows below -30°C for at least a few days each year (and for nearly a month straight so far this winter), I can’t say I have a lot of sympathy. Or maybe I’m just bitter because I never got a day off school due to the cold? But seriously, nothing has to shut down if you plug in the cars at night and bundle up like an astronaut. We’ve been doing it for years.


One still wonders if the probability of this sort of event has been changed by arctic amplification and the ongoing changes to jet stream behaviour as researched and published by Francis and Vavrus.
Just another random event, which will happen periodically as average annual temperatures continue to climb. http://www.huffingtonpost.com/2012/02/15/europe-cold-snap_n_1278569.html
The question in my mind is, “Why did the arctic barf?” Could it be the lessening of temperature and the ensuing pressure difference between the arctic and mid-latitudes?
I’ve been having friendly competitions with your mother this week as to who is harder off this winter…yes, I know you are ;-). Our schools did close today though….we win on that account!
This brings back a couple memories.
When I was a kid going to our one-room school house out in the country, there was only one reason why our school would ever close, and that was when the teacher couldn’t make it there. And we would learn about our school closure only after we had walked a mile and a half to discover that the door was locked and no one was around.
Nearly 50 years ago, a couple years after graduating from college, I started a new job in Hopkins, Minnesota in October. I lived in an apartment with electrical plugins installed in posts across the sidewalk from the cars. I had installed a battery blanket and engine block heater in my old junker. It had faithfully started until…until I really needed it. It was new-years eve and I had great plans for the next day. I knew that there could be trouble, because it had gotten down to around -30°F or so the night before and my car barely started then, even with a warm battery and engine block. So that night it got down to -40°F and the next morning I approached my car with great apprehension. The starter didn’t even make a sound when I turned the key, not even a buzz or clicking noise. Then I opened the hood, for what reason I can’t remember. That’s when I discovered that someone had tripped over my extension cord and disconnected it. Being new-years day, my car didn’t recover from its trauma all day, and it remained there until the next day when I could get someone to come out to give it a boost.
P.S. I moved away from Minneapolis that May and didn’t go back. Where I live now, way south from there, it got down to -20°F two nights ago. (0°F or so has been the lowest it’s gotten around here for many a year.) Early the next morning I tried to start my old John Deere tractor to clear off the foot of snow from our long lane so our neighbors could get to work. Diesel engines don’t like the cold, so I had to wait until the sun warmed it up for three hours or so and my heavy-duty battery charger could do its job. With the 100 amp boost from the charger, the engine did reluctantly start and did reluctantly spurt along for the next twenty minutes or so until enough heat from the engine warmed up the fuel tank located directly above it.
In spite of all that, I know that Atmospheric CO2 will climb above 400ppm this year, and it will be hotter than ever come this July and August, just as it was a few years ago when I was sitting in my RV in a shopping-center parking lot in Bismarck, ND and when the radio announcer said at that very moment that Bismarck had reached a sizzling all-time record high of 115°F. Bismarck, ND, where temperatures have been in the -20 to -40 °F range these last few weeks. Bismarck, where the temperature is now hovering around a balmy -20°F. Bismarck, where the temperature is sure to reach well above 100°F for days or weeks on end this summer.
None of this proves or disproves anything. The only thing that matters is that CO2 will climb above 400ppm this year, which may be far beyond any extended elevated CO2 levels this earth has seen for many, many thousands of years, perhaps even before humans ever existed.
We never had school cancelled due to cold either. Some winters in Northern Ontario it would go below -40 for a few days, or consistently stay in the -30s C, and no school closure. We just bundled up completely and walked off to school like we did every day. I suppose that is why I’m finding the excitement over these recent cold temps rather funny.
By the way, I checked our local weather history and these cold temps were much more common 30 to 40 years back, so I suppose you could argue we’ve been rather spoiled with warmer winters lately.
From what I’ve read, this is exactly what some people predicted as a result of the melting of arctic ice. Seems a pretty clear case of “global warming caused this” to me, even though normally attributing events to a trend is pretty silly.
@various_folk_opining_on_why: my tuppence says that when you’ve got an Arctic death-spiral such a ‘barf’ looks pretty much like an indication that things will not end well…
People are conveniently ignoring the sauna vortex in Australia. Wasn’t 2013 the hottest year ever there?
http://www.skepticalscience.com/2013-was-Australias-hottest-year-warm-for-much-of-the-world.html
How does Australia normally do during an El Nino year anyways?
http://www.skepticalscience.com/Is-a-Powerful-El-Nino-Brewing-in-the-Pacific-Ocean.html
But on a more serious note, Sharknado’s are real! :-)